[Algorithm] - 최소 신장 트리

신장 트리

---

연결 그래프의 부분 그래프로서 그 그래프의 모든 정점과 간선의 부분 집합으로 구성되는 트리로 모든 노드는 적어도 하나의 간선에 연결 ( 단 , 싸이클 X )

 

• 아래 그림은 신장트리를 나타난 예시이다.

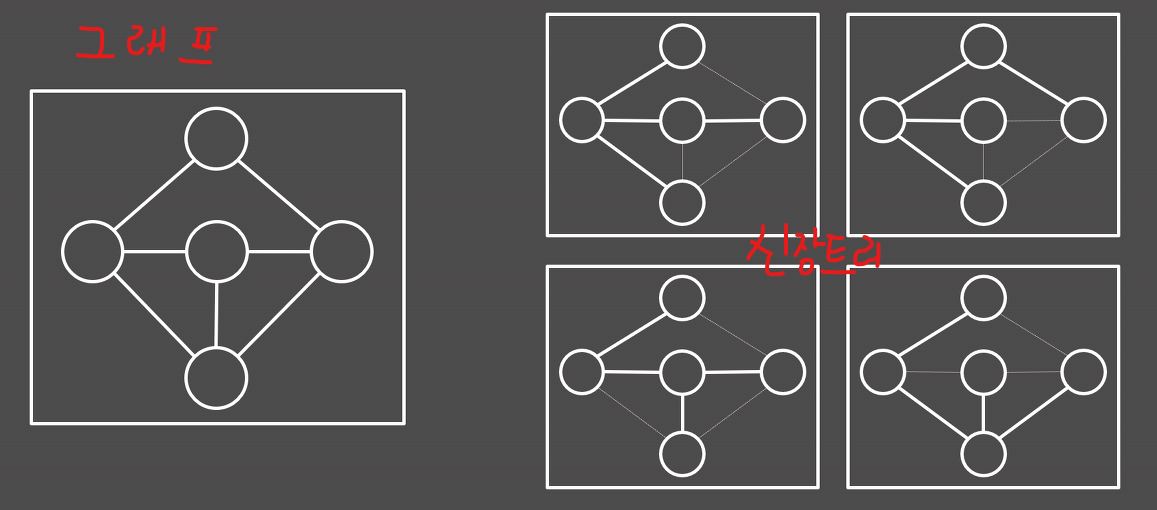
신장트리 예시

• 아래 그림은 신장트리가 아닌 예시이다.
• Node에 Edge가 연결되지 않거나 , Cycle이 발생되어 Tree의 개념을 상실한 경우이다.
• 우측 마지막 그림에서는 Edge가 새롭게 생성된 경우이다.

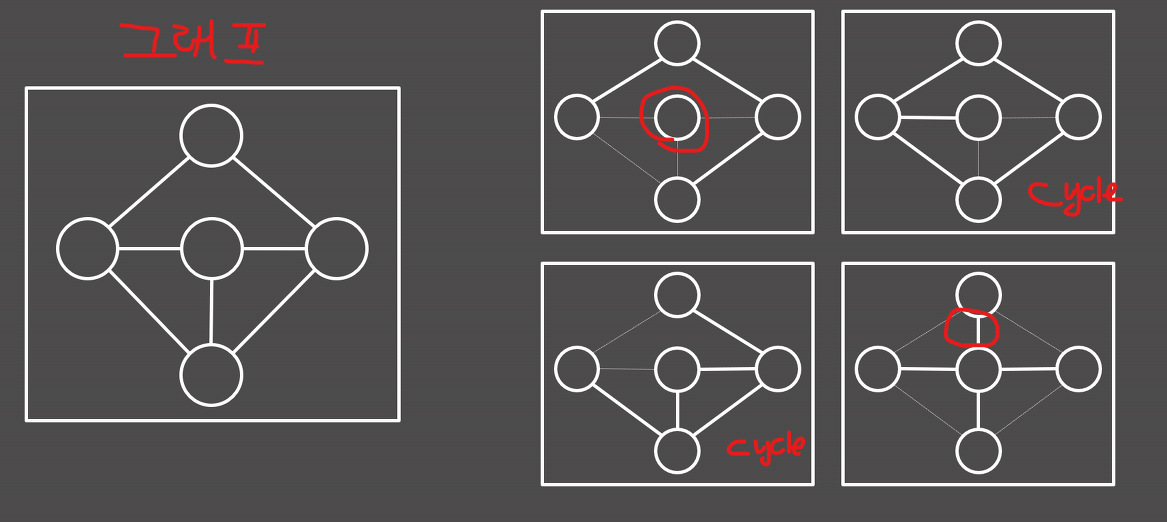
신장트리가 아닌 예시

 

최소 신장 트리

---

Graph Edge에 Cost가 부여된 그래프를 가중치 그래프 또는 네트워크라고 합니다.
이때 Cost란 비용이나 거리를 의미하는 값이 될 수 있습니다.
신장 트리 비용은 신장 트리를 구성하는 모든 간선의 비용 중 최소의 합

• 최소 Cost를 알기 위해서는 Edge들의 가중치를 가장 작은것은 선택해야 한다. -> Heap , 우선 순위 큐

 

1. 크루스칼 ( Union Find Algorithm 필수 )

---

Flood Fill 로 구현은 가능하지만 O ( VE ) 과정이 필요함으로 시간 복잡도가 최악 -> Union Find 알고리즘과 함께 O( ElogE ) 에 구현 가능

 

알고리즘

1. Edge의 Cost가 낮은 순으로 정렬 O( ElogE )

2. 현재 선택한 Edge가 Node A, B를 연결한다고 할 때에 A,B가 같은 그룹이라면 넘어간다. 다른 그룹이라면 같은 그룹으로 설정 후 현재 선택한 Edge를 최소 신장 트리 Edge로 추가

3. 최소 신장 트리가 V-1개의 Edge를 추가하였다면 종료 아니면 1~2 다시 반복 

# 크루스칼 알고리즘
# 최소 신장 트리를 알기 위함
'''
5 7
1 2 4
1 3 3
1 4 3
2 5 8
3 5 5
3 4 4
4 5 6
'''

node , edge = map ( int , input().split() )
edge_list = []
parent_node = [i for i in range( node+1 ) ]

# union_find algrorithm
def find ( node ) :
    if parent_node[node] != node :
        return find(parent_node[node])
    return node

def union ( A , B ) :
    A = find(A)
    B = find(B)

    if A == B :
        return False
    
    if A < B :
        parent_node[B] = A
    else :
        parent_node[A] = B

    return True

# 크루스칼
for _ in range( edge ) :
    start , end , cost = map( int , input().split() )
    edge_list.append( [start , end , cost] )

edge_list = sorted ( edge_list , key = lambda x : x[2] )

for edges in edge_list :
    start , end , cost = edges
    if union( start ,end ) :
        print ( start , end )

 

Union Find Algorithm

• 2개의 Node가 동일한 그룹인지 여부 파악
• find, union 연산의 시간복잡도는 평균 아커만함수의 역함수를 가진다. O(1)이라고 보면 된다.

# union_find algrorithm
def find ( node ) :
    if parent_node[node] != node :
        return find(parent_node[node])
    return node

def union ( A , B ) :
    A = find(A)
    B = find(B)

    if A == B :
        return False
    
    if A < B :
        parent_node[B] = A
    else :
        parent_node[A] = B

    return True
       
parent_node = [i for i in range( node+1 ) ]

 

2. 프림

---

우선 순위 Queue를 이용하여 구현 O( ElogE )
시작할 지점의 Node를 임의로 선택한 뒤 선택할 수 있는 Edge 중에서 최소를 선택하여 구현한다.

 

알고리즘

1. 임의 Node하나를 선택하여 최소 신장 트리에 추가하여 준다. Node와 연결된 Edge들은 모두 우선 순위 Queue에 추가한다.

2. 우선 순위 Queue에 있는 Edge 중 가장 Cost가 낮은 Edge를 선택

3. 현재 Edge가 최소 신장 Tree에 포함된 Node들을 연결하고 있다면 넘어간다. 연결하고 있지 않다면, Node들의 Edge 추가 및 최소 신장 트리에 추가

4. 최소 신장 트리 갯수가 V-1 이 될 때 까지 1~3 반복

# 프림 알고리즘
'''
5 7
1 2 4
1 3 3
1 4 3
2 5 8
3 5 5
3 4 4
4 5 6
'''

import sys
import heapq
input = sys.stdin.readline

v , e = map( int , input().split() )
adj = [ [] for _ in range(v+1) ]
heapq_list = []
start = 1
answer = [False] * (v+1)
answer[start] = True
cnt = 0

for _ in range ( e ) :
    edge_start , edge_end , cost = map ( int , input().split() )
    adj[edge_start].append( [edge_end,cost])
    adj[edge_end].append( [edge_start,cost])

for temp in adj[start] :
    edge_end , cost = temp
    heapq.heappush(heapq_list , ( cost , start , edge_end ))

while(cnt < v-1) :
    cost ,edge_start , edge_end = heapq.heappop(heapq_list)

    if answer[edge_end] :
        continue

    print ( edge_end )
    answer[edge_end] = True
    cnt += 1
    for temp in adj[edge_end] :
        edge_end , cost = temp
        heapq.heappush(heapq_list , ( cost , edge_start , edge_end ))

 

 

BOJ 1368 - 물대기

---

IDEA

각 Node별로 물을 연결할 수 있는 최소의 값!

-> 최소 신장 트리

주의할 점이 최소 신장 트리 알고리즘으로 구하기 위해서 우물은 어떻게 처리해야 하는가?

-> index 0 번을 우물로 처리

 

# BOJ 1368 - 물대기
# 최소의 비용으로 각 노드별로 연결하기
# 크루스칼
import sys
input = sys.stdin.readline

def find( node ) :
    if parent[node] != node :
        return find(parent[node])
    return node

def union( a , b ) :
    a = find(a)
    b = find(b) 
    if a == b :
        return False
    
    if a < b :
        parent[b] = a
    else :
        parent[a] = b
    return True

n = int(input()) 
edge_list = []
parent = [i for i in range(n+1)]
cnt , answer = 0 , 0

for i in range( 1 , n+1 ) :
    cost = int(input())
    edge_list.append( [0,i,cost] )
    edge_list.append( [i,0,cost] )

for i in range( n ) :
    for index , value in enumerate(  map(int, input().split())  ) :
        if value == 0 :
            continue
        edge_list.append( [i+1,index+1,value])

edge_list = sorted( edge_list , key = lambda x : x[2] )

for edge in edge_list :
    if cnt > n-1 :
        break
    start , end , cost = edge
    if union ( start , end ) :
        answer += cost
        cnt += 1

print ( answer )

 

참조 : https://blog.encrypted.gg/1024 / https://0x15.tistory.com/34